[기초] 2. Optimization최적화기법/최적화: 매개변수 초기화 및 갱신

 

이 글은 필자가 "밑바닥부터 시작하는 딥러닝 1"을 보고 헷갈리는 부분이나 다시 보면 좋을만한 부분들을 위주로 정리한 글입니다.

🪀 해결이 되지 않은 부분

1. Gradient Descent vs. Stochastic Gradient Descent
   1. GD: 전체 데이터 update
   2. SGD: Batch 기준으로 데이터 update 

      

      https://seamless.tistory.com/38

2. Loss function의 derivation이 잘 와닿지 않음/그래프 양상 이해안감.

🪀 최적화Optimization 틀

: 최적의 매개변수 구하기 = 매개변수를 갱신해가면서 최적의 매개변수를 찾는다.

1. 결과에 따른 손실 함수(Loss function): 전체 퍼셉트론 결과에 따른 손실을 구하는 것을 말한다.
2. 매개변수/가중치 갱신
   1. 매개변수 초깃값 설정
   2. 오차역전법으로 가중치 매개변수의 기울기 계산
   3. 기울어진 방향으로 가중치의 값을 갱신

🪀 최적화Optimization 방법론

1. 매개변수 초깃값 방법론
   1. Xavier 초깃값
   2. He 초깃값
2. 매개변수 갱신 방법론
   1. 이동관점
      1. Stochastic Gradient Descent(SGD)
      2. Momentum
   2. 학습률 감소 관점: AdaGrad
   3. 이동 + 학습률 감소 관점: Adam
   4. 요즘: 일반적으로 SGD, Adam

🪀 매개변수 초깃값 설정

가중치의 대칭적인 구조를 무너뜨리려면 초깃값을 무작위로 설정해야 한다.

• Xavier 초깃값: 각 층의 활성화값들을 광범위하게 분포시킬 목적으로 가중치의 적절한 분포 착지, Sigmoid나 tanh 등의 S자 모양 곡선
  • 앞 계층의 노드가 n개라면 표준편차가 1/(n)^(1/2)인 분포 사용 (xavier_normal_, xavier_uniform_이 존재한다.)

   def initialize_weights(self):
        # track all layers
        for m in self.modules():
            if isinstance(m, torch.nn.Conv2d):
                torch.nn.init.xavier_normal_(m.weight)
            elif isinstance(m, torch.nn.BatchNorm2d):
                torch.nn.init.xavier_normal_(m.weight)
            elif isinstance(m, torch.nn.Linear):
                torch.nn.init.xavier_normal_(m.weight)
            if m.bias is not None:
                torch.nn.init.constant_(m.bias, 0)

• He 초깃값: ReLU에 특화된 초깃값
  • 앞 계층의 노드가 n개라면 표준편차가 (2/n)^(1/2)인 분포 사용

🪀 매개변수 갱신

매개변수 갱신 방법론 들어가기 전...

• 학습률 감소: 학습을 진행하면서 학습률을 점차 줄어드는 방법

$$W: weight, \frac{\partial L}{\partial W}: Derivation\; of\; loss\; function, \eta: learning\;rate(hyper parameter)$$

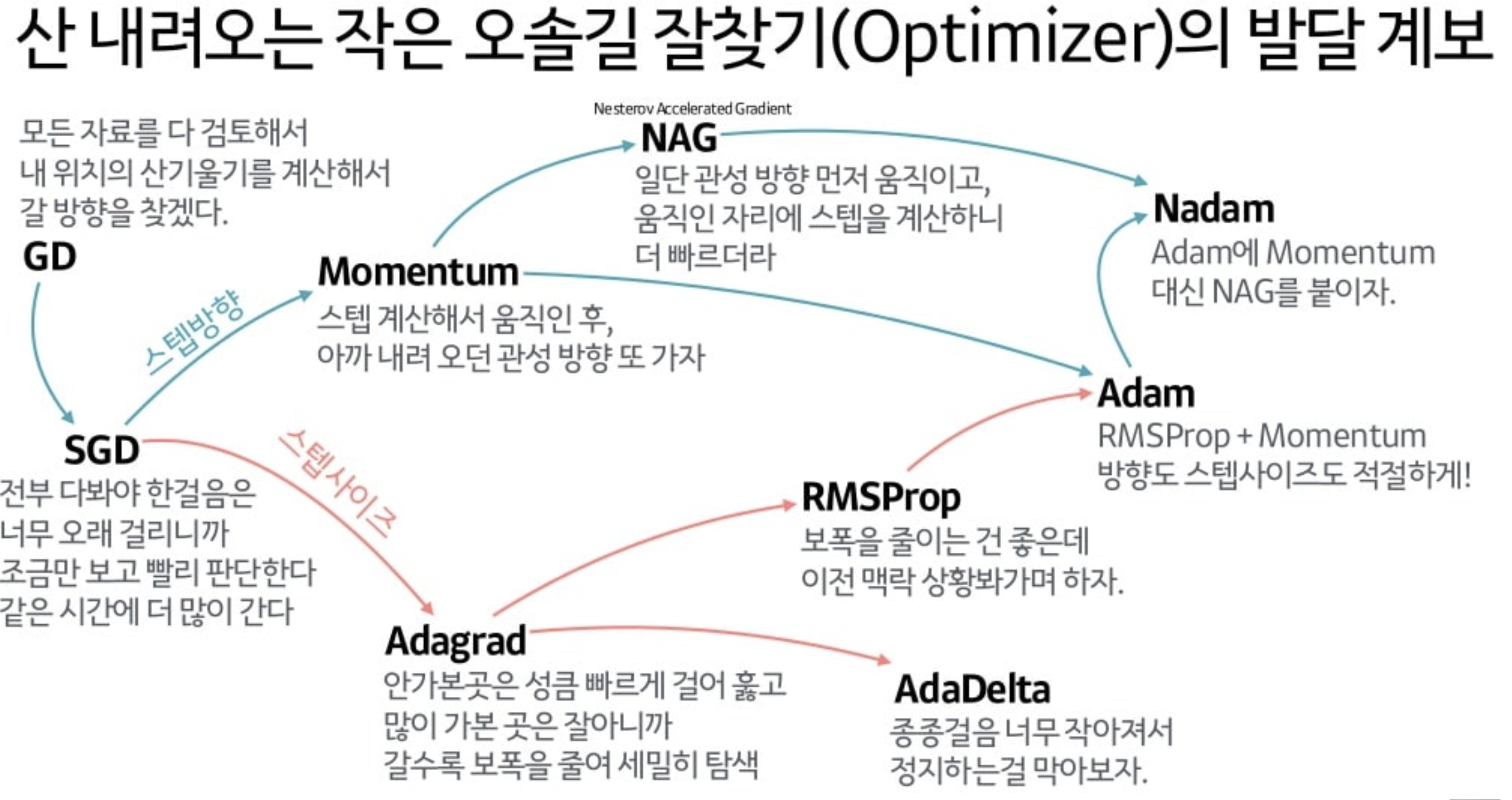
0. Gradient Descent(GD)

• Gradient: 경사, Derivation: 미분값
• Gradient Descent: 비용함수의 값을 극소화, 전체 데이터에 적용
• Gradient Ascent: 비용함수의 값을 극대화
• Gradient Vanishing: 미분값이 감소되면서 오히려 Gradient descent와 ascent에 도움이 되지 않는 경우가 존재한다. 대표적인 예시로는 Sigmoid function이 존재한다.

1. Stochastic Gradient Descent(SGD)

$$W \longleftarrow W - \eta \frac{\partial L}{\partial W}$$

• Stochastic Gradient Descent: 배치로 작용
• 기울어진 방향으로 일정한 거리만 가겠다는 단순한 방법
• Cons
  • 지그재그로 이동하는 경로가 비효율적
  • 이런 경향을 나타내는 비등방성 함수에서는 탐색 경로가 비효율적    

    

    https://www.researchgate.net/figure/A-typical-energy-landscape-depicting-position-of-several-local-minima-which-indicate-the_fig3_45900660

2. Momentum

$$W \longleftarrow W + v$$

$$v \longleftarrow \alpha v - \eta \frac{\partial L}{\partial W}$$

• 기울어진 방향으로 일정한 거리만 가겠다는 방법 기울기에 따라 다른 이동 거리를 이야기
  • 모멘텀의 원리: 공이 그릇의 곡면(기울기)에 따라 구르듯 움직인다.
• Pros: 지그재그 정도가 '덜'하다.

3. AdaGrad

$$W \longleftarrow W - \eta \frac{1}{\sqrt{h}}\frac{\partial L}{\partial W}$$

$$h \longleftarrow h + \frac{\partial L}{\partial W} \odot \frac{\partial L}{\partial W} $$

• 학습률 감소 관점) 매개변수 '전체'의 학습률 값을 일괄적으로 낮추는 방법, '각각의' 매개변수에 '맞춤형 값'
  
  • h: 과거의 기울기 값을 제곱하여 계속 더하는 방식, 매개변수의 원소 중 많이 움직인 원소는 학습률이 낮아진다.
• Pros: 최솟값을 향해 효율적으로 움직임

4. Adam

• 이동 관점) 그릇 바닥을 구르는 듯한 움직임 + 학습률 감소 관점) 매개변수의 원소마다 적응적으로 갱신 정도를 조정
• Pros: 하이퍼파라미터의 '편향 보정'이 진행된다.

 

🪀 Sum up...

https://www.slideshare.net/yongho/ss-79607172/