[Basic] Activation Function/Loss Function/Evaluation metric

본 글은 필자의 이해를 돕기 위해 작성된 글입니다. 참고 링크: 링크1

🐤Loss Function 과 Evaluation Metric 차이점

간단히 말해서 Loss function은 딥러닝 모델 학습시 성능을 높이기 위해 minimize/maximize 시켜야 하는 지표이고, Evaluation metric은 여러 딥러닝 모델들 중에 좋은 성능을 확인하기 위해 쓰이는 지표입니다.

 예를 들어 classification 문제라 하면 모델의 loss function은 대체적으로 crossentropyloss 으로 분류의 지표를 표시한다면 모델 들 간의 성능을 확인하기 위해서는 evaluation metric이 accuracy가 되어야 한다.

 딥러닝 모델의 parameter estimation method 중 하나인 Maximum likelihood Estimation(MLE)는 이를 구현하기 위해 Maximum A Posterior Estimation(MAP)를 활용한다. 참고링크

🐤 Activation Function 종류

• ReLU $$max(0,x)$$
• Softmax $$S(x) = - \frac{1}{1+e^{-x}}$$
  • 중간 층의 출력값에 대표적으로 사용되며, 0~1 사이의 값을 출력합니다. 주로 binary classification에 사용되어 0.5보다 크면 해당한다고 분류됩니다.
• Sigmoid $$\sigma(z)_i = \frac{e^{z_i}}{\sum_{j=1}^{K}e^{z_j}}$$
  • 출력함수에 최종 class 별 0~1사이의 값으로 출력됩니다. categorical classification에 사용되어 가장 높은 probability를 가지면 해당한다고 분류합니다.
  • 왜 Classification에서는 BCE가 어울리는가? Gradient 적용시 Classification의 마지막 activation function인 sigmoid function에서 MSE는 Gradient vanishing이 적용된다.

 

🐤 Loss Function 종류

Loss는 Negative Log likelihood를 바탕으로 정의되며 대표적으로 MSE, BCE가 존재한다.

• Negative Log likelihood (NLL) $$L(y) = -log(y)$$

Loss function	MSE	BCE
Prediction	$$\hat{y}$$	$$p$$
Output distribution Assumption	Gaussian distribution (sigma=1)	Bernoulli Distribution

 

•  CrossEntropy(CE)
  • Bernoulli Distribution, Probability $$ P(\hat{y}=y |X) = p^y (1-p)^{1-y}$$
  • Binary Cross-entropy(BCE) $$ L(\hat{y}) =-( y \log (p) + (1-y) \log(1-p))$$
    • $$Loss = -\log P = - \log ( p^y (1-p)^{1-y}) = -( y \log (p) + (1-y) \log(1-p))$$
  • Categorical Cross-entropy $$L(\hat{y}, y) = - \sum_k^K y^{(k)}log \; \hat{y}^{(k)}$$

• Mean Squared Error(MSE) 
  • Gaussian/Normal Distribution(sigma=1), Probability $$P(\hat{y}=y |X) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp^{-\frac{1}{2} (\frac{(y - \hat{y})^2}{\sigma^2})}$$
  • $$ Loss = - \log P = \frac{1}{2} \log (2\pi) + \log(\sigma) + \frac{(y - \hat{y})^2}{\sigma^2} = \frac{1}{2} \log (2\pi) + (y - \hat{y})^2  \approx  (y - \hat{y})^2 $$
  • $$MSE Loss = L(\hat{y}, y) = \frac{1}{N} \sum_{i=1}^N (y_i - \hat{y}_i)^2$$
• 번외
  
  • Multitask Loss
    • Regularization loss: for robust model add regularization loss and get multitask loss ex. L1, L2 Regularization loss 
    • Mask R-CNN loss function $$Loss = L_{cls} + L_{BBox} + L_{Mask}$$
    • Variational Auto-Encoder $$Loss = L_{Reconstruct} + L_{Regularization}$$
      • Reconstruction loss: Loss to check of how well the image has been reconstructed from the input

 

🐤 Evalution Metric 종류

https://en.wikipedia.org/wiki/Confusion_matrix

Confusion matrix→ Accuracy, F1 score

• Accuracy 
  • $$Accuracy = \frac{TP+TN}{P+N}$$
• F1 Score
  • $$F1 Score  = \frac{2TP}{2TP + FP+FN}$$
  • Precision과 Recall의 조화평균이며 주로 분류 클래스 간 데이터가 심각한 불균형을 이루는 경우에 사용된다.

IoU → Precision/Recall → PR → AP → IoU에 따른 mAP

• IoU(Intersection over Union)
  • $$IoU = \frac{TP}{TP+FP} = \frac{TP}{All detections}$$
  • IoU가 threshold를 만족한다면(0.5 이상이면) 제대로 검출(TP)되었다고 판단한다. 만약 0.5 미만이면 잘못 검출(FP)되었다고 판단한다.
• Confusion matrix에 따른 Precision/Recall
  • Precision정밀도: 검출 결과들 중 옳게 검출한 비율 $$Precision = \frac{TP}{TP+FP} = \frac{TP}{All detections}$$ 
  • Recall재현율: 실제 옳게 검출된 결과물 중 제대로 예측한 것의 비율 $$Recall = \frac{TP}{TP+FN} = \frac{TP}{All Ground truths}$$
  • Precision-Recall 곡선(PR곡선): Precision, Recall은 서로 반비례 관계를 가지며 PR 곡선에서는 recall 값의 변화에 따른 precision 값을 확인할 수 있다.
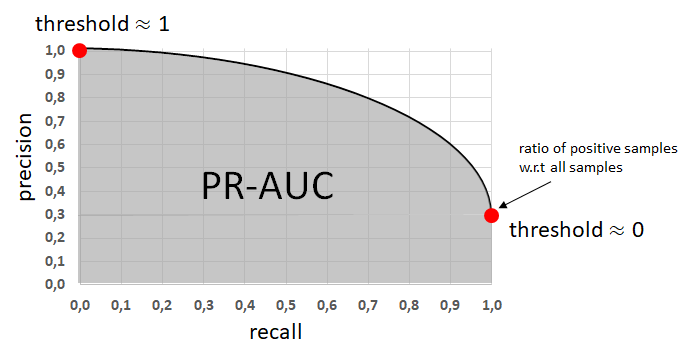
    • AP/AR(Average Precision, mAP/mAR) = PR-AUC $$ AP(:PR-AUC) = \int_0^1 PR(rec) d(rec) $$ PR-곡선 아래의 영역으로, PR-AUC가 높을수록 완벽한 분류기이다.
      
      • Object detection의 대표적인 성능 지표로 사용된다.
      • mAP(mean Average Precision): 각 클래스당 AP의 평균

https://ichi.pro/ko/precision-mich-recalle-daehan-jiggwanjeog-in-ihae-65549580633255