데이터 예측에 실행되는 순서들
Linear Model선형모델 의 간단한 개요
선형모델은 말그대로 Linear선을 가지고 모델을 짜는 알고리즘을 말합니다.
풀어서 말하면 입력값 X와 출력값Y간의 관계를 일차함수(선형 함수)로 모델링합니다.
입력값 X와 출력값Y는 각각 행렬의 형태로 하나의 x값에 대응되는 y값이 하나씩 존재합니다.

여기서 feature가 p개이면 이런 형태로 X,Y값을 나타낼 수 있습니다. 하지만 저희는 하나의 파라미터에 영향을 미친다는 가정하에 이렇게 나타낼 수 있고, 결국 y = a*x+b의 형태에 다다르게 되어 입력값 X, 출력값 Y가 있으면 이 둘의 관계에 걸맞는 최선의 a, b를 구하는 것이 저희의 목표가 될 것입니다.
최선의 a, b를 구하는 것이 Linear Regression선형 회귀를 통하여 하나의 식이 만들어지게 되고
이렇게 나타나게 됩니다.

하나의 x값에 대응하는 y값을 좌표로 나타내었다면 빨간 색 선은 이를 통하여 유추해낸 선입니다.
만약 예측해야 할 x값이 0이 된다면 저희는 y값이 5라고 예측합니다.
간단히 코드로 구현해본다면,
from sklearn.linear_model import LinearRegression
//------train set, test set 준비-------//
model = LinearRegression()
model.fit(X_train,y_train)
prediction = model.predict(X_test)
print(prediction)
간단한 과정은 이렇게 됩니다.
Loss Function손실 함수
아직 저희는 모델 만들기 단계에 있습니다.
최선의 모델을 만드는 도중에 평가는 필요한데, 이는 손실함수를 통하여 우리의 손실이 어느정도인지 파악을 하게 됩니다.
손실함수의 종류는 다양합니다. MSE, RMSE, Cross Entropy Loss 등등을 말할 수 있는데요,
이 Linear Model은 MSE를 씁니다.
우선 손실을 구해야 하는데 이는 기존의 출력값에서 추론값을 뺀 것을 말하는데, 그림으로 나타내보면

Error = y(기존의 출력값) - yhat(추론한 값)
여기서 y값이 yhat보다 큰지 , 작은지에 따라서 +, - 값이 될 것입니다.
Mean Squared Error는 부호에서 자유롭고, 오류의 값을 증폭하기 위해(파악하기 쉽게) Error에 제곱을 한 형태를 띄어, 표본의 개수 n으로 나누어 표현됩니다.

이렇게 구해진 오류들을 통하여 최적의 a,b를 찾고 싶으면 Linear Regression에서는
Gradient Descent경사 하강법을 이용하게 됩니다. 그 전에 Optimization최적화 기법을 간단히 알아보도록 하죠.
Optimization최적화 기법
Gradient Descent경사 하강법
기울기를 통한 Error 조정이라고 간단하게 말할 수 있는데요, Gradient Descent은 사실 3가지의 방법으로 나뉘어 실현이 되지만 저희는 그 중에 가장 기본적인 Gradient Descent경사하강법에 대하여 말하고자 합니다.
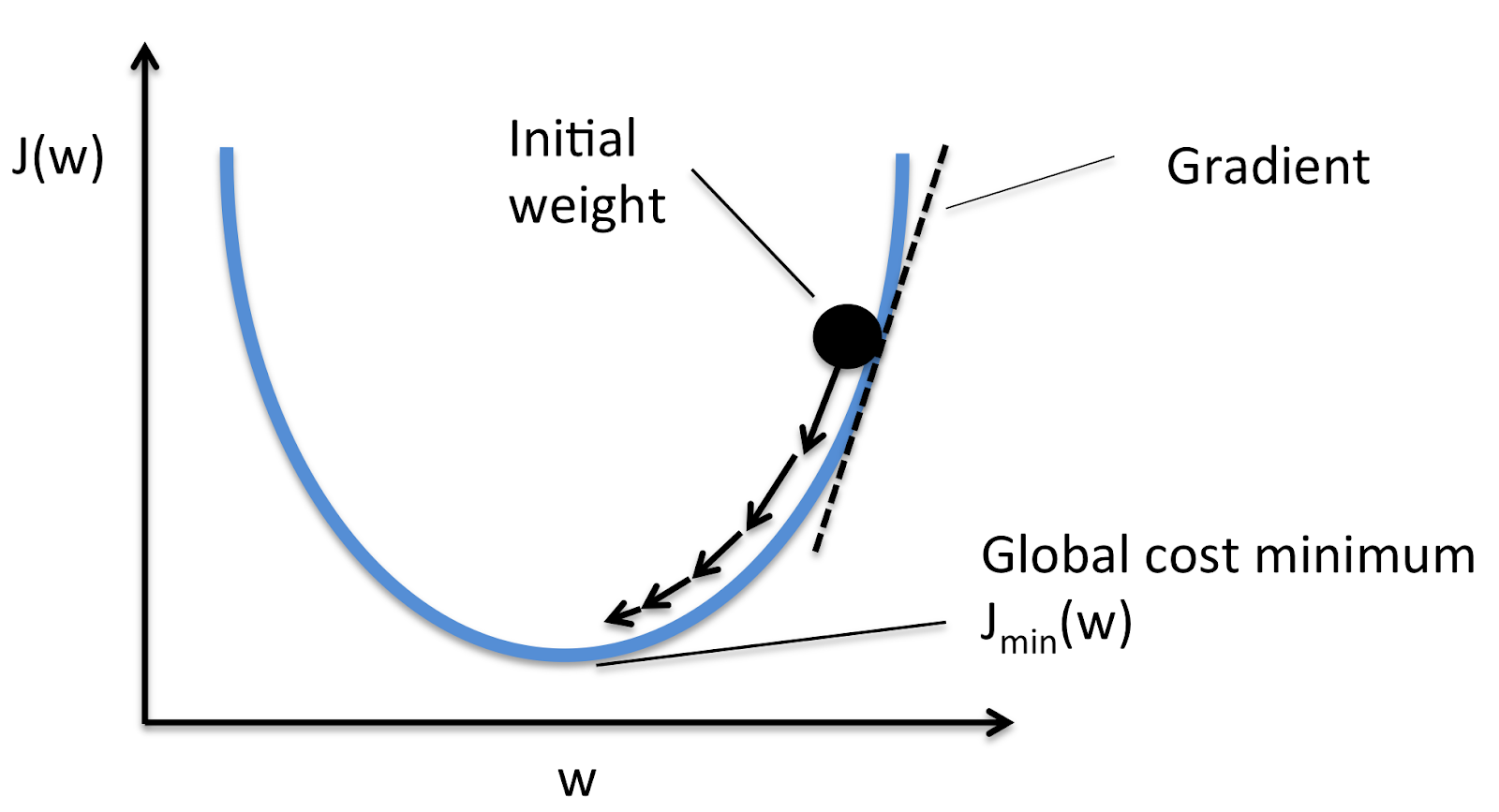
간단히 말해서 기존의 값에서 기울기에 따라 조금씩 내려가서 결국에 Error가 가장 작은 지점에 도달하는 방법인데요,
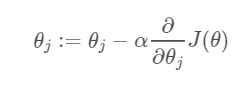
하이퍼 파라미터(우리가 스스로 값을 정해야 하는 피라미터) 인 알파 : Learning Rate라 하고
그 뒤에 J(theta)를 미분한 값이 기울기인 것을 알 수 있어서
만약 미분값이 양수라면 이는 J(theta)가 증가하고 있는 쪽의 일부이므로 왼쪽으로 보내지고
미분값이 음수라면 이는 J(theta)가 감소하고 있는 쪽의 일부이므로 오른쪽으로 보내지게 됩니다.
이 미분값은 값 자체가 중요한 게 아닌 어느쪽으로 이동했느냐가 중요하고 여기서 관건은 Learning Rate입니다.
Learning Rate의 값을 어떻게 정하느냐에 따라서 많이 이동하고, 적게 이동하는 것이 결정되기 때문에
초기에 크게 정해놓았으면 파라미터를 정하는 과정에서 왔다갔다 하는 일들이 발생하여 최적의 값을 찾게 되는데 느리고, 작게 정해 놓으면 오히려 조금씩 가서 최적의 값을 찾는데 느리게 구해지는 단점이 있습니다.
이를 조정해야 하는 저희로써는 신중하게 결정해야 합니다.
위에 보시는 값은 파라미터 1개에 대해서 말씀드린 것이고
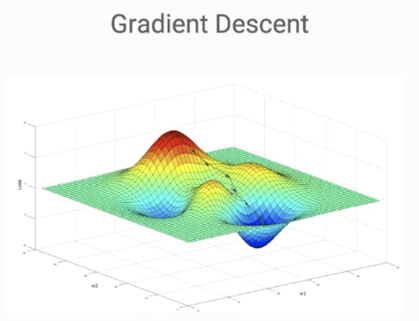
아래는 파라미터 2개가 서로 연관되어 있어 동시에 고려해야 하는 경우, 2개를 모두 고려하기 위해 3차원 좌표를 이용해
미끄럼틀 타듯이 밑쪽으로 내려가서 최적의 파라미터를 정하는 경우를 찾아볼 수 있습니다.
'AI, Deep Learning Basics > Basic' 카테고리의 다른 글
| [NN] PyTorch 함수 모음 (0) | 2021.12.29 |
|---|---|
| [Pytorch] 모델 만들 때 초기값을 설정해주는 이유 (0) | 2021.11.24 |
| [Deep Learning]여러 개의 훈련 데이터set로 딥러닝 기반 신경망 알고리즘 적용/Neural Networks and Deep Learning/in multiple training examples/in several hidden layer (0) | 2019.03.26 |
| [Deep Learning]하나의 훈련 데이터로 본 딥러닝 기반 신경망 알고리즘 적용 (0) | 2019.03.25 |
| [AI] Neural Networks and Deep Learning 단원 정리 (0) | 2019.03.18 |
![[Machine Learning] Linear Model선형모델/LinearRegression선형회귀/LinearClassification선형분류](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FzktFz%2Fbtqu0TwLqBv%2FShbCBg3YnHiieLbuP7BbtK%2Fimg.png)